Recordareis que en el anterior artículo se definió el “error” de una encuesta, se enseñó a calcular la correspondiente desviación típica y, por último se explicó cómo usar estos datos para establecer la fiabilidad de una encuestadora, comparando sus predicciones con la cruda realidad.
Sin embargo, aquel método “bruto” tenía un grave problema que lo hacía casi inaplicable (al menos, a las Generales españolas): solo tenía sentido si la encuesta “sospechosa” era muy próxima a los comicios: si hablamos de dos o tres semanas de distancia, como es habitual, siempre era posible alegar que…
“En ese tiempo se mueve mucho voto, y por tanto es lógico que la encuestadora se equivoque bastante. No hay porque ver fantasmas”.
En efecto, se mueve voto: es evidente que las expectativas electorales de un partido pueden cambiar bastante en las de últimas semanas de campaña. Pero… ¿Tanto? Centrándonos en la siempre polémica Metroscopia, ¿sus catastróficos errores de predicción a un mes vista del 20-D, pueden ser fruto simplemente, de variaciones masivas en el ánimo de los votantes? ¿La subida Podemos (3.6 puntos) y, SOBRE TODO, la hecatombe de C’s (8.7 puntos), en menos de un mes que nos muestra esta encuestadora, son algo estadísticamente verosímil?
Metodología
Evidentemente, la respuesta dependerá de cuanto sea la variación media mensual de ese partido. Si un partido se mantuviera, un suponer, estable en un 20% durante todo un año, sería muy difícil de justificar una caída “repentina” de 10 puntos. Así que lo primero que necesitamos es algo con lo que comparar. Y no solo para un partido en concreto, sino para el conjunto.
Y para ello, ¿qué mejor que tomar los datos de la propia Metroscopia a lo largo de 2015 y establecer un promedio de variación mensual en la intención de voto?
| Fecha | Podemos | PSOE | PP | C’s | Otros | IU |
| I-E | 28,2 | 23,5 | 19,3 | 8,1 | 15,7 | 5,3 |
| I-F | 27,7 | 18,3 | 20,9 | 12,2 | 14,4 | 6,5 |
| I-M | 22,5 | 20,2 | 18,6 | 18,4 | 14,7 | 5,6 |
| I-A | 22,1 | 21,9 | 18,5 | 19,4 | 10,8 | 5 |
| I-J | 21,5 | 23 | 20,8 | 13 | 13,9 | 4,1 |
| I-JL | 21,5 | 22,5 | 23,1 | 15 | 14 | 4 |
| III-JL | 18,1 | 23,5 | 23,1 | 16 | 13,7 | 5,6 |
| I-S | 18,6 | 24,6 | 23,1 | 16,1 | 12,3 | 5 |
| I-O | 14,1 | 23,5 | 23,4 | 21,5 | 11,9 | 5,6 |
| I-N | 17 | 21 | 23,5 | 22,5 | 9,7 | 6,3 |
| IV-N | 17,1 | 22,5 | 22,7 | 22,6 | 9,9 | 5,2 |
| II-D | 19,1 | 21 | 25,5 | 19,1 | 11,4 | 5 |
| Elecciones | 20,7 | 22 | 28,7 | 13,9 | 11 | 3,7 |
Podemos, por ejemplo, tenía una intención de voto en enero del 28,2 y en febrero bajó al 27.7, así que la tasa de variación en ese periodo para Podemos era de (27,7-28,2)/1=-0,5 Puntos/mes. Es decir, perdía intención de voto a un ritmo de medio punto mensual. En cambio, y por comparar, en las dos semanas transcurridas entre las dos encuestas publicadas en julio, Podemos pasa del 21,5 al 18,1, así que el ritmo de variación era entonces de (18,1-21,5)/0.5=-6.8 puntos/mensuales (ignoro qué paranormal suceso justifica ese desplome).
Pues bien, el problema que se nos presenta es unificar todas estas variaciones mensuales: “sumar” los resultados de Podemos, C’s, PSOE, PP… a fin de obtener un valor promedio que poder comparar con lo ocurrido el 20-D. Y digo “sumarlas”, entre comillas, porque obviamente no podemos hacerlo: el resultado sería cero (lo que unos ganan, otros lo pierden). Afortunadamente, para calcular ese “global” existen al menos dos métodos distintos.
1) El clásico: sumar los valores absolutos de la variación mensual de cada partido
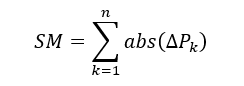
2) Uno un poco más “exótico”: aplicar Pitágoras.
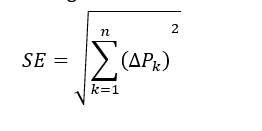
A la primera forma se la llama “distancia Manhattan”, a la segunda “distancia euclidea”. Es interesante saber que ambos métodos, aunque pueden dar resultados numéricamente muy distintos, son estadísticamente más o menos equivalentes: el segundo es más sensible a los cambios bruscos en un solo partido. En este caso, y para que quede claro que no hay trampa ni cartón, se han realizado el cálculo por AMBOS métodos.
Resultados
Pues bien, cuando se meten todos los datos en una tabla Excel se obtiene lo siguiente:
-La variación media en la intención de voto global para las encuestas de Metroscopia es (según Manhattan) 8,55 puntos/mes. La desviación típica es 4.76 puntos/mes
-La variación media en la intención de voto global para las encuestas de Metroscopia es (euclidea) 4,51 puntos/mes. La desviación típica es 2,5 puntos/mes
Conclusiones
Vamos a centrarnos en el método Manhattan, que es más intuitivo:
Resulta que si comparamos el resultado global del 20-D con el de la encuesta preelectoral publicada por Metroscopia a finales de noviembre obtenemos que en solo un mes, y suponiéndola veraz, las variaciones acumuladas de todos los partidos (especialmente C’s y Podemos) dan… ¿Estáis sentados?
¡¡¡28,5 puntos/mes!!!.
Es decir, que, de ser cierto lo publicado, en los 23-25 días que pasaron desde que se recogieron los datos de la citada encuesta hasta las elecciones, la velocidad con la que cambiaba la intención de voto CUADRUPLICÓ lo normal. De hecho, la variación de C’s por sí solo, con una caída de 11 puntos/mes, ya se sale de las tablas.
Pues bien, solo queda ver hasta qué punto esto anómalo. Y para eso aplicamos exactamente los mismos criterios explicados en el artículo anterior. Concretamente, la desviación sobre el promedio es la friolera de 4,2 veces la desviación típica, y eso significa que…
La probabilidad de que el error en la encuesta del 29/11/15 de Metroscopia fuera fruto de variaciones reales en la intención de voto durante la campaña es del: 0.0027%. Es decir, una entre 37000.
Si repetimos los cálculos para el método euclideo, obtenemos un resultado prácticamente idéntico: la probabilidad resulta ser del 0.0022%. Es decir, una entre 45000: perfectamente coherente con lo anterior.
Es cierto, que una campaña electoral no es un periodo “normal” y que es de suponer que el voto tiene más tendencia a variar de forma más brusca y “nerviosa” (aunque hay estudios sociológicos que lo niegan, afirmando que la influencia de la campaña en el votante es casi nula). Pero, ¿tanto como para contradecir estos contundentes números? Dejo a cada cual que saque sus propias conclusiones.
—
Nota: a la hora de hacer los cálculos, se ha descartado la última encuesta preelectoral de Metroscopia, por mostrar variaciones demasiado bruscas y oportunas (seamos diplomáticos) respecto a la anterior. No obstante, de incluirla, la probabilidad pasa a ser de 1 contra 200, aproximadamente.
Un artículo de Victorino García.

























































































































































































Tu opinión
Existen unas normas para comentar que si no se cumplen conllevan la expulsión inmediata y permanente de la web.
EM no se responsabiliza de las opiniones de sus usuarios.
¿Quieres apoyarnos? Hazte Patrón y consigue acceso exclusivo a los paneles.